Robust Phase Retrieval with Prior Knowledge
Robust Phase Retrieval with Prior Knowledge
Output
1 Introduction
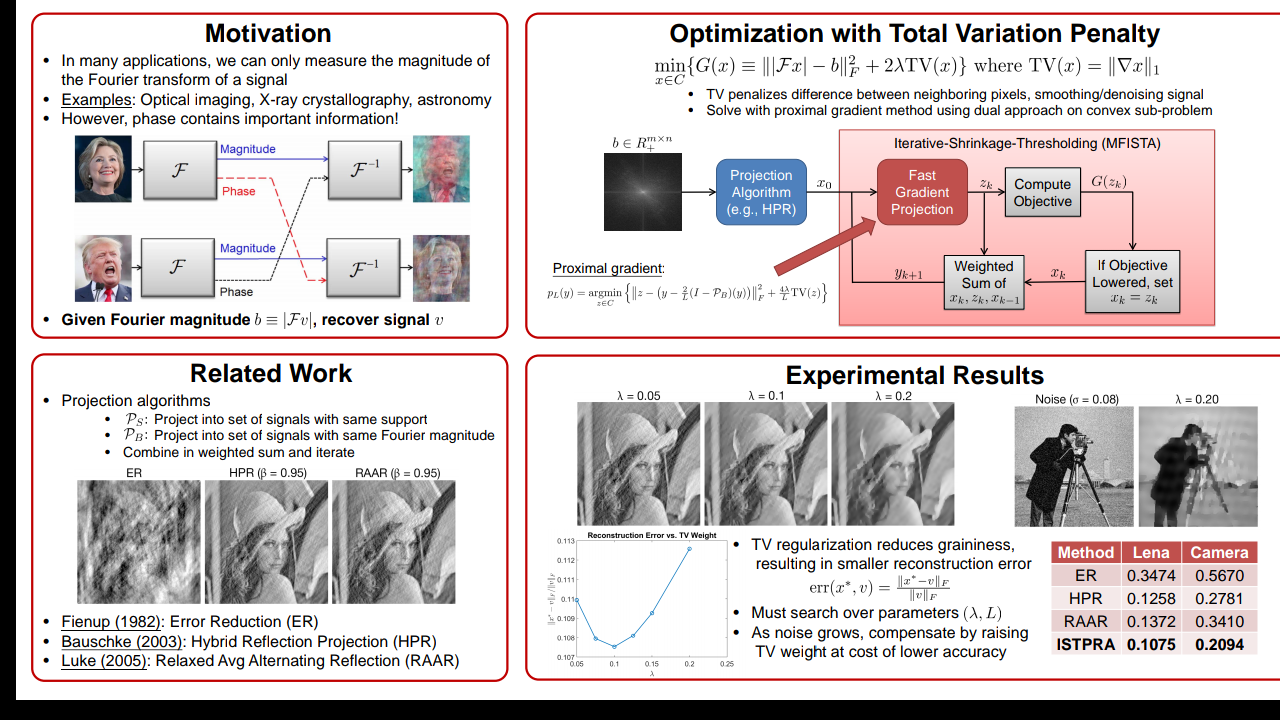
In many imaging applications, one can only measure the power spectral den-sity (the magnitude of the Fourier transform) and not the phase of the signalof interest. For example, in optical settings, devices like CCD cameras only capture the photon flux, so important information stored in the phase is lost.The challenge is to reconstruct the original signal from measurements of its Fourier magnitude. This problem, known as phase retrieval, arises in many scientific and engineering applications, including optics, crystallography, and astronomy.
2 Problem Description
Suppose x = (x1, . . . , xN ) is a non-negative signal, and denote by F : x → F the operator that returns its N-point discrete Fourier transform (DFT). We observe b = (b1, . . . , bN ) ∈ R N+ , the magnitude of the Fourier transform of the signal, and wish to find x that satisfies |Fx| = b. Phase retrieval can be
posed as the optimization problem
min x{f(|Fx| − b)} (1)
3 Project Goals
My goal is to reconstruct the signal x ∈ R N + as accurately as possible, where accuracy is determined by the peak signal-to-noise ratio (PSNR). First, I will implement the classic error reduction (ER) and hybrid input-output (HIO) algorithms described in [SWL16]. At every iteration k, these algorithms solve 1 with f(x) = ||x||2 2 via a gradient descent update followed by a projection
onto the support, i.e. S k such that xi = 0 for all i /∈ S
k . For pixels outside the support, ER sets x
k+1
i = 0 uniformly, while HIO incorporates feedback
information from the current iteration’s x
ki
.Then, time permitting, I will consider two extensions of the optimiza-
tion problem: a weighted prior and a regularization function with a known
proximal gradient. In the first case, I include a total variation penalty on x
min x ( αf(|Fx| − b) + (1 − α)NX−1 n=1 (xn+1 − xn))
, s.t. x ≥ 0 (2)
where the weight α ∈ [0, 1] is chosen by cross-validation. In the second case, I add a regularization term r(x) min x {f(|Fx| − b) + r(x)}, s.t. x ≥ 0 (3)
where the proximal operator of r is defined as
prox (z) = arg min x r(x) + 1 2||x − z||22
This allows me to use proximal gradient methods to iteratively optimize the objective. Some regularizers I will try are the l1 norm, the l2 norm, and a strict bound on the cardinality (r(x) = 0 for card(x) ≤ s and ∞ elsewhere), which is useful in situations involving sparse coding. I will compare the accuracy and runtime of these extensions with the ER and HIO algorithms.4 Implementation
I plan to implement my solution in MatLAB and Python and test it on publicly available high-resolution digital photographs from SCIEN.
References
[CSV13] E. J. Candes, T. Strohmer, and V. Voroninski. PhaseLift: Ex- act and stable signal recovery from magnitude measurements via convex programming. Communications on Pure and Applied
Mathematics, 66(8):1241–1274, 2013.
[Fie82] J. R. Fienup. Phase retrieval algorithms: a comparison. Applied optics, 21(15):2758–2769, 1982.
[JEH15] K. Jaganathan, Y. C. Eldar, and B. Hassibi. Phase re-trieval: an overview of recent developments. arXiv preprint arXiv:1510.07713, 2015.
[MAOM13] Y. L. Montagner, E. D. Angelini, and J-C. Olivo-Marin. Phase retrieval with sparsity priors and application to microscopy video reconstruction. In 2013 IEEE 10th International Symposium on Biomedical Imaging, pages 604–607. IEEE, 2013. [SWL16] L. Shi, G. Wetzstein, and T. J. Lane. A flexible phase re- trieval framework for flux-limited coherent x-ray imaging. arXiv
preprint arXiv:1606.01195, 2016.



Comments
Post a Comment